| Karva notation was developed specifically for gene expression programming
(GEP) and consists of a universal way of representing any mathematical or logical expression that can be represented as a tree. Here we are going to
introduce it briefly, but you can find a more detailed explanation on the
following sub-sections of this chapter – The
Architecture of GEP Programs and The
Architecture of GEP-RNC Programs. The chromosomes of gene expression programming code for one or more K-expressions, and each K-expression is encoded in a gene. Genes and K-expressions are very easy to interpret. For example, the gene:
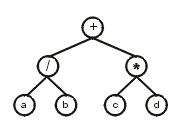
0123456 can be represented as a diagram or expression tree (ET):
The translation of the gene into the corresponding ET is straightforward: The first element in the gene (position 0) corresponds to the root of the ET; then, below that node, are attached as many nodes as there are arguments to that function (two, in this case); then these nodes are filled consecutively with the elements in the gene (in this case, positions 1 and 2), and so forth. The process is repeated until a line composed of only terminals is formed (in this case, the third line).
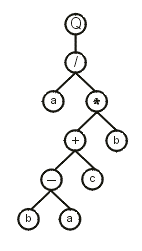
Usually the genes evolved by GEP are more complex than the gene presented above, with noncoding regions at the end. Consider the following gene (the head is shown in blue):
01234567890123456 where “Q” represents the square root function. This gene has a head of length 8 and a tail of length 9. Note that the head contains both functions and terminals, whereas the tail contains exclusively terminals. The translation of such genes is done exactly as in the previous example, obtaining:
Note that, in this case, not all the elements in the gene were used to construct the ET, as the translation ends whenever a line containing only terminals is formed. In this case, the gene ends at position 16 whereas the K-expression ends at position 9.
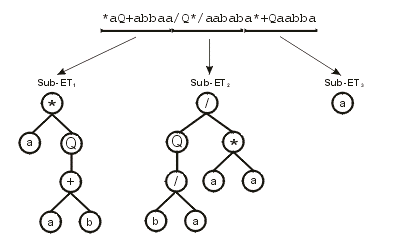
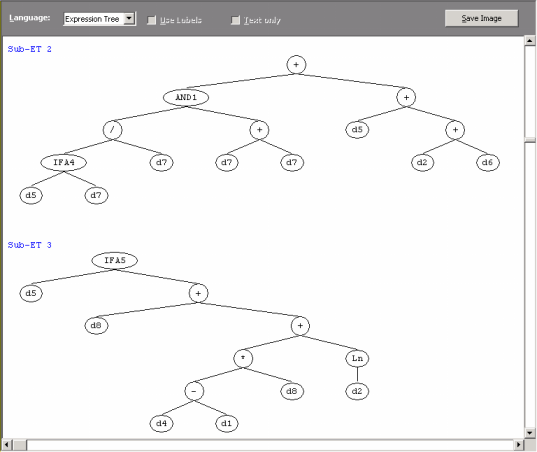
012345678012345678012345678 encodes the following sub-ETs:
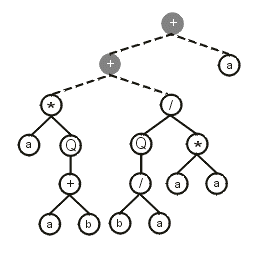
Then the sub-ETs are afterwards linked by one of the available linking functions. For instance, if the linking function were addition, then the following program would be obtained:
Note that the ET above can be easily linearized into a single K-expression:
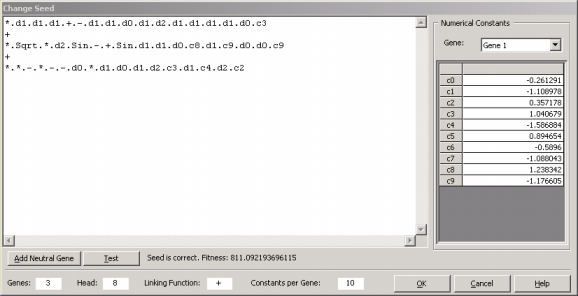
01234567890123456 These manipulations are important in order to fully explore all the features of APS, especially the Change Seed method, which allows you to change or create a particular program and then use this program to breed even better programs.
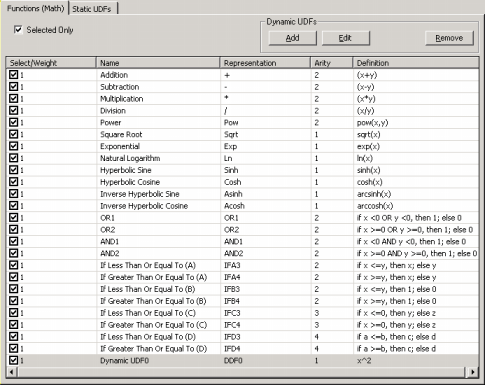
Obviously you’ll need to know the symbols used to represent all the 70 built-in mathematical functions of APS 3.0 in Karva if you wish to create seed programs with them. But, as will be shown next, they are quite easy to learn as most of the times their names obey common rules of naming mathematical functions in programming languages.
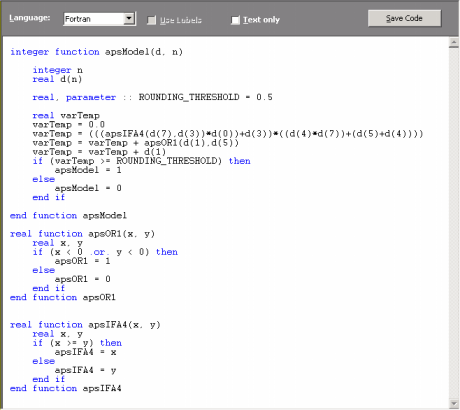
So, Automatic Problem Solver 3.0 evolves models in its native Karva code, but the models evolved by APS in its native language can be automatically parsed into visually appealing expression trees, allowing a quicker and more complete understanding of their mathematical intricacies.
Additionally, Automatic Problem Solver 3.0 offers a total of eight built-in grammars so that the models evolved by APS in its native language can be automatically translated into the most commonly used programming languages (C, C++, C#, Visual Basic, VB.Net, Java, Java Script, and Fortran). This code can then be used in other applications.
And finally, Automatic Problem Solver 3.0 allows also the design of User Defined Grammars so that the models evolved by APS in its native language can be automatically translated into the programming language of your choice if you happen to prefer a programming language not already covered by the
eight built-in grammars of APS 3.0 (C, C++, C#, Visual Basic, VB.Net, Java, Java Script,
and Fortran). |