• Addition (+): x+y
• Subtraction (-): x-y
• Multiplication (*): x*y
• Division (/): x/y
• Floating-point Remainder (Mod): mod(x,y)
• Power (Pow): pow(x,y)

Basic mathematical functions of one argument:

• Square Root (Sqrt): sqrt(x)
• e^x (Exp): exp(x)
• 10^x (Pow10): pow(10,x)
• Natural Logarithm (Ln): ln(x)
• Logarithm Base 10 (Log): log(x)
• Logistic (Logi): logistic(x)
• Floor (Floor): floor(x)
• Ceiling (Ceil): ceil(x)
• Absolute Value (Abs): abs(x)
• Inverse (Inv): 1/x
• No Operation (Nop): x
• Negation (Neg): -x

Trigonometric functions (x is in radians):

• Sine (Sin): sin(x)
• Cosine (Cos): cos(x)
• Tangent (Tan): tan(x)
• Cosecant (Csc): csc(x)
• Secant (Sec): sec(x)
• Cotangent (Cot): cot(x)

Inverse trigonometric functions:

• Arcsine (Asin): arcsin(x)
• Arccosine (Acos): arccos(x)
• Arctangent (Atan): arctan(x)
• Arccosecant (Acsc): arccsc(x)
• Arcsecant (Asec): arcsec(x)
• Arccotangent (Acot): arccot(x)

Hyperbolic functions:

• Hyperbolic Sine (Sinh): sinh(x)
• Hyperbolic Cosine (Cosh): cosh(x)
• Hyperbolic Tangent (Tanh): tanh(x)
• Hyperbolic Cosecant (Csch): csch(x)
• Hyperbolic Secant (Sech): sech(x)
• Hyperbolic Cotangent (Coth): coth(x)

Inverse hyperbolic functions:

• Inverse Hyperbolic Sine (Asinh): arcsinh(x)
• Inverse Hyperbolic Cosine (Acosh): arccosh(x)
• Inverse Hyperbolic Tangent (Atanh): arctanh(x)
• Inverse Hyperbolic Cosecant (Acsch): arccsch(x)
• Inverse Hyperbolic Secant (Asech): arcsech(x)
• Inverse Hyperbolic Cotangent (Acoth): arccoth(x)

Comparison 0/1 functions of two arguments:

• OR1 (OR1): if x < 0 OR y < 0, then 1; else 0
• OR2 (OR2): if x >= 0 OR y >= 0, then 1; else 0
• AND1 (AND1): if x < 0 AND y < 0, then 1; else 0
• AND2 (AND2): if x >= 0 AND y >= 0, then 1; else 0

Comparison IF THEN ELSE functions of two arguments (series A):

• If Less Than (IFA1): if x < y, then x; else y
• If Greater Than (IFA2): if x > y, then x; else y
• If Less Than Or Equal To (IFA3): if x <= y, then x; else y
• If Greater Than Or Equal To (IFA4): if x >= y, then x; else y
• If Equal To (IFA5): if x = y, then x; else y
• If Not Equal To (IFA6): if x != y, then x; else y

Comparison 0/1 IF THEN ELSE functions of two arguments (series B):

• If Less Than (IFB1): if x < y, then 1; else 0
• If Greater Than (IFB2): if x > y, then 1; else 0
• If Less Than Or Equal To (IFB3): if x <= y, then 1; else 0
• If Greater Than Or Equal To (IFB4): if x >= y, then 1; else 0
• If Equal To (IFB5): if x = y, then 1; else 0
• If Not Equal To (IFB6): if x != y, then 1; else 0

Comparison IF THEN ELSE functions of three arguments (series C):

• If Less Than (IFC1): if x < 0, then y; else z
• If Greater Than (IFC2): if x > 0, then y; else z
• If Less Than Or Equal To (IFC3): if x <= 0, then y; else z
• If Greater Than Or Equal To (IFC4): if x >= 0, then y; else z
• If Equal To (IFC5): if x = 0, then y; else z
• If Not Equal To (IFC6): if x != 0, then y; else z

Comparison IF THEN ELSE functions of four arguments (series D):

• If Less Than (IFD1): if a < b, then c; else d
• If Greater Than (IFD2): if a > b, then c; else d
• If Less Than Or Equal To (IFD3): if a <= b, then c; else d
• If Greater Than Or Equal To (IFD4): if a >= b, then c; else d
• If Equal To (IFD5): if a = b, then c; else d
• If Not Equal To (IFD6): if a != b, then c; else d

By selecting the Functions (Math) Tab in the Functions Panel, you have full access to the 70 built-in mathematical functions of APS 3.0. Here is also the place where you can add Dynamic UDFs (DDFs) to your modeling kit.

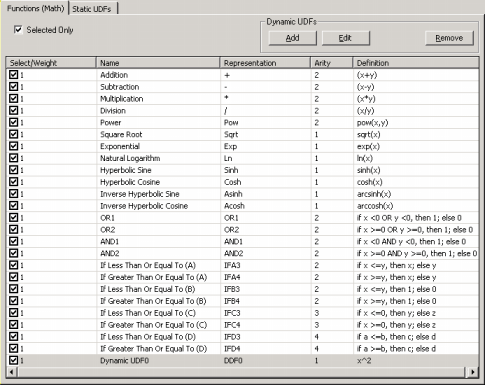
To select a function, just check the box on the left. By default, the weight of each function is 1, but you can increase the probability of a function being included in your models by increasing its weight in the Select/Weight column. The weight property is very important for a successful modeling, as the overall number of functions used in a run must be well balanced with the number of terminals or variables in your data. For instance, if you are modeling data with dozens of variables (that is, huge embedding dimensions) and using only the four arithmetical operators, you must weight proportionately the representation of each function in the function set, otherwise the creation of complex models will be seriously compromised. A good rule of thumb is to have at least as many functions in the function set as there are variables.

To add a DDF to your modeling kit, just click the Add button on the Dynamic UDFs frame and the DDF editor appears.

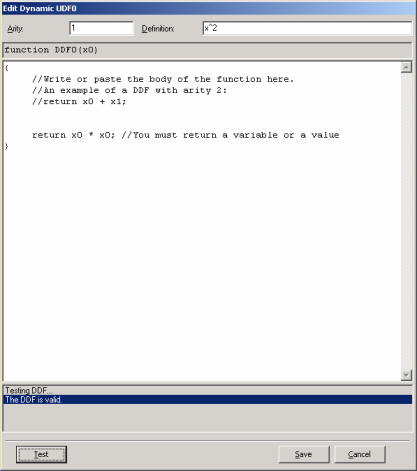
By choosing the arity (minimum is 1 and maximum is 4) in the Arity box, the function header appears below. Then you just have to write the body of the function in the code editor. The code must be in JavaScript and can be conveniently tested for compiling errors.

In the Definition box, you can write a brief description of the function for your future reference. The text you write here will appear in the Definition column.

Dynamic UDFs are extremely powerful and interesting tools as they are treated exactly like the built-in functions of APS and therefore can be used to model all kinds of relationships between variables or complex expressions. For instance, you can design a DDF so that it will model the sum of four expressions, that is, DDF = (expression 1) + (expression 2) + (expression 3) + (expression 4), where the value of each expression will depend on the context of the DDF in the expression tree. A note of caution, though, although extremely interesting, DDFs decrease considerably the speed of the algorithm and therefore we advise you to choose your functions from the wide set of APS 3.0 built-in functions.