The successful creation of Function Finding models requires the use of very sharp modeling tools. The most important are listed below.
Data Screening Engine
The data screening engine of APS 3.0 checks the validity of all the data sets used both in the creation and testing of the model.
Function finding problems require data files with numerical inputs of any kind, but it is common for the files to have missing or nominal values which render them useless for modeling or testing. APS 3.0 data screening engine can help you identify these faulty samples and correct them.
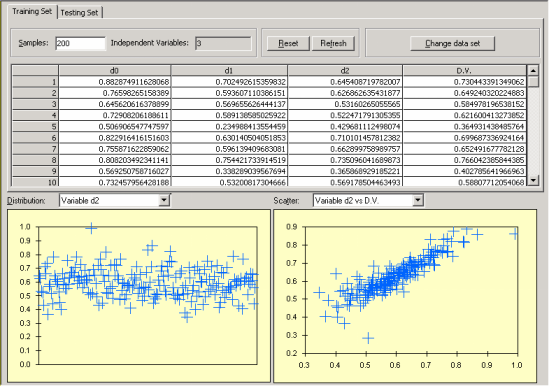
Data Visualization Tool
The data visualization tool of APS 3.0 enables you to analyze the distribution of all the inputs and to spot simple relationships between the independent variables and the dependent variable.
The visualization of both the distribution and relationships between variables is a valuable modeling tool as it can help you detect outliers or simple relationships between your variables that can be used to evolve more efficient models.
Built-in Fitness Functions
Automatic Problem Solver 3.0 offers a total of 11 built-in fitness functions based on well-known statistical functions.
Fitness functions are fundamental modeling tools for they determine the nature of the search landscape. And different fitness functions open and explore different paths in the solution space. The fitness functions of APS 3.0 are named as follows:
Relative with SR,
Relative/Hits, Absolute with
SR, Absolute/Hits,
R-square, MSE,
RMSE, MAE,
RSE, RRSE, and
RAE.
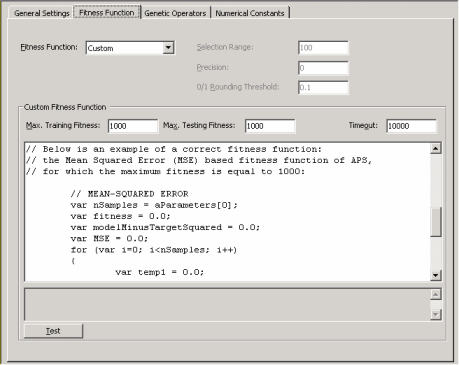
User Defined Fitness Functions
Despite the wide set of APS built-in fitness functions, some users sometimes want to experiment with fitness functions of their own. Automatic Problem Solver 3.0 gives the user the possibility of creating custom tailored fitness functions and evolve models with
them.
The code for the custom fitness function must be in JavaScript and is written in the Custom Fitness Function window and can be tested before evolving a model with it.
Built-in Mathematical Functions
Automatic Problem Solver 3.0 offers a total of 70 built-in mathematical
functions. This wide set of mathematical functions allows the evolution of complex and rigorous models quickly built with the most appropriate functions.
From the simple arithmetic operators to complex mathematical functions available in most programming languages to more complex mathematical functions commonly used by engineers and scientists, the modeling algorithms of APS 3.0 enable you the integration of the most appropriate functions in your models.
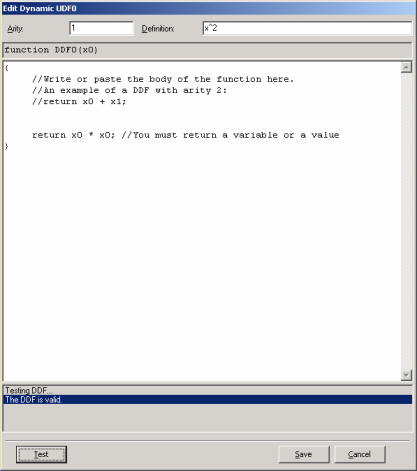
Dynamic User Defined Functions (DDFs)
Despite the wide set of APS built-in mathematical
functions, some users sometimes want to model with different ones. APS 3.0 gives the user the possibility of creating custom tailored functions and evolve models with them. A note of warning though: the use of dynamic UDFs slows considerably the evolutionary process and therefore should be used with moderation.
The code for the DDFs must be in JavaScript and is written in the Edit DDF window (in the Functions Panel, select the Functions (Math) Tab and then click Add in the Dynamic UDFs tool box).
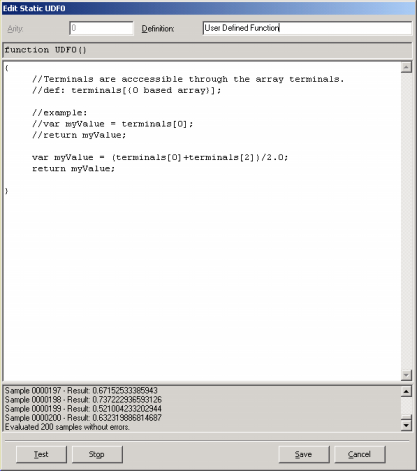
Static User Defined Functions (UDFs)
Sometimes it is possible to spot relatively simple relationships between certain variables in your data, and APS 3.0 allows you to use this information to build custom tailored functions (UDFs). These functions allow the discovery of more complex models composed of several simpler models.
The code for the UDFs must be in JavaScript and is written in the Edit UDF window (in the Functions Panel, select the Static UDFs Tab and then click Add in the Static UDFs tool box).
Learning Algorithms
Automatic Problem Solver 3.0 is equipped with two different algorithms for evolving complex nonlinear regression models.
The first is the fastest and simplest of the two. And because it is also the most efficient, this algorithm is the default in APS 3.0. The second algorithm is very similar to the first, with the difference that it gives the user the possibility of choosing the range and type of numerical constants that will be used during the learning process.
In order to evolve models using the second algorithm, select Numerical Constants in the Settings Panel and then check the box that activates this algorithm. You will notice that additional parameters become available, including a small set of genetic operators especially developed for handling numerical constants (if you are not familiar with these operators, please use the default values for they work very well in all cases).
Monitoring the Modeling Process
Automatic Problem Solver 3.0 allows you to monitor the modeling
process by plotting the essential parameters of a run during the discovery process, including
the fitness and R-square of the best-of-generation model and average fitness.
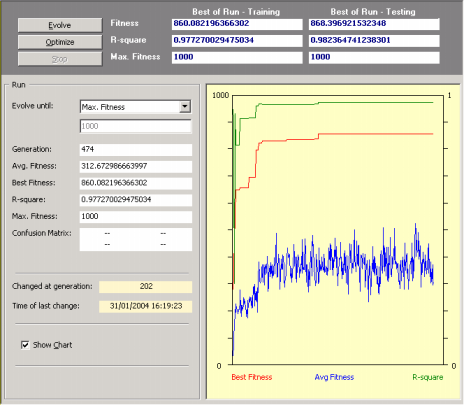
The evolutionary process can be stopped whenever you are satisfied with the results by pressing the Stop button or you can use one of the stop criteria of APS
and have APS stop automatically after a certain condition had been
met.
When the evolutionary process stops, the best-of-run model is ready either for analysis or scoring. And if you are still not happy with the results, you can still try to fine-tune the evolved model by pressing the Optimize button and repeat this process until you are completely satisfied with your model.
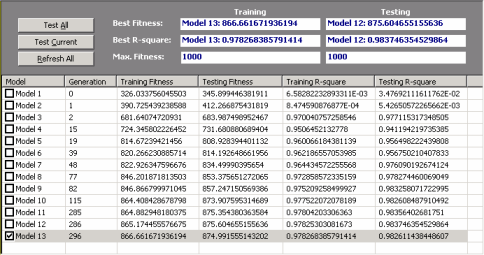
Analyzing Intermediate Models
Automatic Problem Solver 3.0 gives you the possibility of gaining some insights into the modeling process by analyzing all the best-of-generation intermediate models.
All the best-of-generation models discovered during a run are saved and you can pick them up for analysis at the
History Panel by checking the model you are interested in. Each of these intermediate models can then be analyzed exactly as you do for the best-of-run model, that is, you can check their performance in the testing set, check their vital statistics, automatically generate code with them, visualize their parse trees, use them as seed to create better models from them and so forth.
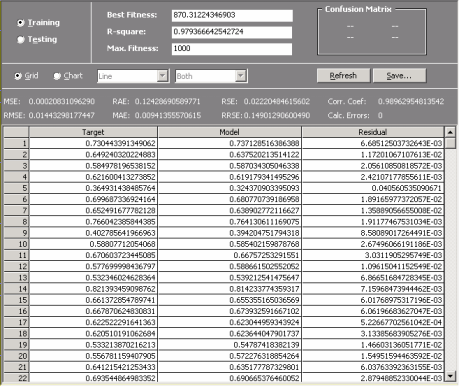
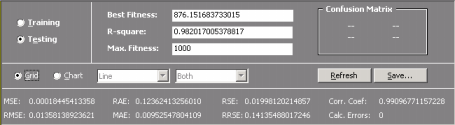
Comparing Actual and Predicted Values
Automatic Problem Solver 3.0 offers two different ways of analyzing and comparing the output of your model with the actual or target values both for the training and testing sets.
In the first, the target or actual values are listed in a table side by side with the predicted values.
In the second, the target and predicted values are plotted in a chart for easy visualization.
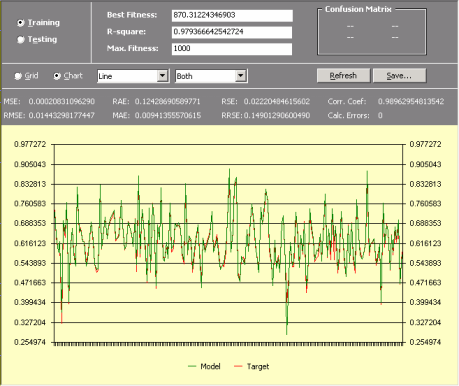
Essential Statistics
Automatic Problem Solver 3.0 allows a quick and easy assessment of a wide set of
statistical
functions. Most of them are immediately computed and shown every time you check the Results Panel
(for instance, fitness, mean squared error,
root mean squared error,
mean absolute error,
relative squared error,
root relative squared
error, relative absolute
error, R-square,
and correlation
coefficient).
Modeling from Seed
Automatic Problem Solver 3.0 allows the use of an existing model (which could have been either generated by APS or by another modeling tool) as the starting point of an evolutionary process so that more complex, finely tuned models could be created.
For models created outside of APS 3.0 or for APS 3.0 models modified by the user, the starting model or seed is fed to the algorithm through the Change Seed window where both the fitness and structural soundness of the model are tested.
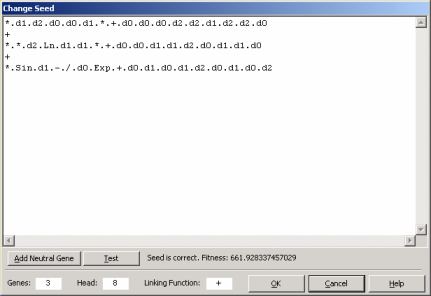
Then, in the Run Panel, by clicking the Optimize button, an evolutionary process starts in which all the subsequent models will be descendants of the seed you introduced. A note of caution though: if your seed has a very small fitness, you risk loosing it early in the run as better models could be randomly created by APS 3.0 and your seed would, most probably, not be selected for breeding new models. If your seed has zero fitness, though, you will receive a warning so that you could
modify your seed until it becomes a viable seed capable of breeding new models.
For models created in the APS 3.0 environment, the seed is fed to the algorithm every time you click the Optimize button during modeling, with the seed (in this case, the best model of the previous run) being introduced automatically by
APS.

Adding a Neutral Gene
The addition of a neutral gene to a seed might seem, at first sight, the wrong thing to do as most of the times we are interested in creating efficient and parsimonious models. But one should look at this as modeling in progress as, for really complex phenomena, it is not uncommon to approximate a complex function progressively.
Thus, being able of introducing extra terms to your seed is a powerful modeling tool and APS 3.0 allows you to do that through the Change Seed window.
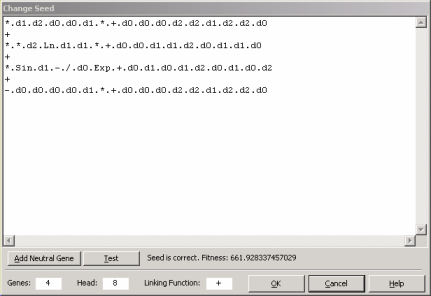
Here, by pressing the Add Neutral Gene button, you will see a neutral gene being added to your model. By doing this, you are giving the learning algorithm more room to play and, hopefully, a better, more complex program will evolve.
Neutral genes can also be introduced automatically by APS 3.0 using the Complexity Increase
Engine.
Complexity Increase Engine
Automatic Problem Solver 3.0 also allows you to introduce neutral genes automatically by activating the Complexity Increase
Engine in the Settings Panel -> General Settings Tab.
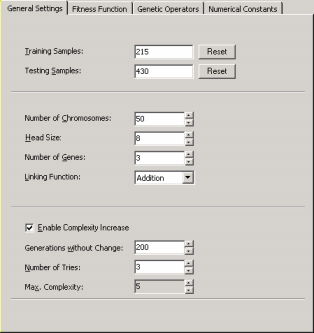
Whenever you are using the Complexity Increase Engine of APS 3.0, you must fill the Generations Without Change box to set the period of time you think acceptable for evolution to occur without improvement in best fitness, after which
a mass extinction or a neutral gene (an extra term) is automatically added to your model; the Number of Tries box corresponds to
the number of consecutive evolutionary epochs (defined by the
parameter Generations Without Change) you will allow before a
neutral gene is introduced in all evolving models; in the Max. Complexity box you write the maximum number of terms (genes) you’ll allow in your model and no other terms will be introduced beyond this threshold.
The Complexity Increase Engine of APS 3.0 might be a very powerful modeling tool, especially for Time Series Prediction where good models could take longer to come by, but you must be careful not to create excessively complex models for, most of the times, a greater complexity does not imply a greater efficiency.
Visualizing Models as Parse Trees
Automatic Problem Solver 3.0 comes equipped with a parse tree maker that automatically converts your models into diagram representations or
parse trees.
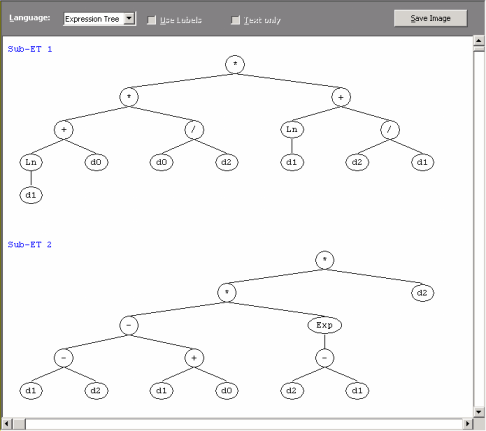
Indeed, all the models evolved by APS in its native Karva language can be automatically parsed into visually appealing expression trees, allowing a quicker and more complete understanding of their mathematical intricacies.
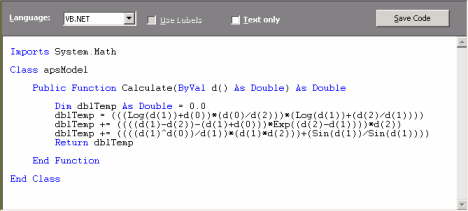
Generating Code Automatically Using APS Built-in Grammars
Automatic Problem Solver 3.0 offers a total of eight built-in grammars so that the models evolved by APS in its native
Karva language can be automatically translated into the most commonly used programming languages (C, C++, C#, Visual Basic, VB.Net, Java, Java Script,
and Fortran). This code can then be used in other applications.
Generating Code Automatically Using User Defined Grammars
Automatic Problem Solver 3.0 allows the design of User Defined Grammars so that the models evolved by APS in its native
Karva language can be automatically translated into the programming language of your choice if you happen to prefer a programming language not already covered by the
eight built-in grammars of APS 3.0 (C, C++, C#, Visual Basic, VB.Net, Java, Java Script,
and Fortran).
As an illustration, the C++ grammar of APS 3.0 is shown here. Other grammars may be easily created using this or other APS built-in grammar as reference.
Scoring Engine
Automatic Problem Solver 3.0 comes equipped with a scoring engine for scoring your databases or text files in the APS environment.
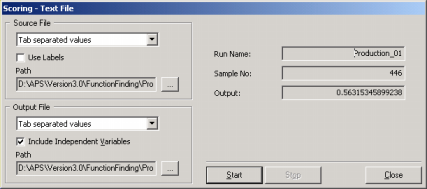
After its creation, a model is usually used multiple times to make predictions or extrapolations. The scoring engine of APS 3.0 allows the immediate scoring of your databases as soon as a model is created, saving the scores to a database or text file.
|
















