| |
 |
 |
 |
Last update: February 19, 2014
|
|
|
 |
 |
 |
|
Root Relative Squared Error
The root relative squared error (RRSE) is relative to what it would have been if a simple predictor had been used. More specifically, this simple predictor is just the average of the actual values. Thus, the relative squared error takes the total squared error and normalizes it by dividing by the total squared error of the simple predictor.
By taking the square root of the
relative squared error one reduces the error to the same dimensions as the quantity being predicted.
Mathematically, the root relative squared error Ei of an individual model
i is evaluated by the equation:
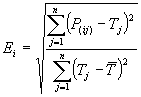
where P(ij) is the value predicted by
the individual model i for record j (out of n
records); Tj is the target value for record
j; and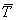 is
given by the formula: is
given by the formula:
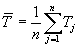
For a perfect fit, the numerator is equal to 0 and Ei
= 0. So, the Ei index ranges from 0 to infinity, with 0
corresponding to the ideal.
See Also:
Related Tutorials:
Related Videos:
|
|
|
|
|

