|
Log Odds Analysis
 |
Log Odds and Logistic Regression |
The Log Odds Chart is central to the Logistic Regression Model.
It’s with its aid that the slope and intercept of the
Logistic Regression Model
are calculated. And the algorithm is quite simple. As mentioned previously,
it’s quantile-based and, in fact, just a few additional calculations
are required to evaluate the regression parameters.
So, based on the Quantile Table, one first evaluates the
odds
ratio for all the bins (you have access to all the values on the
Log
Odds Table under Odds Ratio). Then the natural logarithm of this
ratio (or the Log Odds) is evaluated
(the Log Odds values are also shown on the Log Odds Table under Log
Odds).

Note, however, that there might be a problem in the evaluation of
the log odds if there are bins with zero positive cases. But this
problem can be easily fixed with standard techniques. Although rare for large datasets, it
can sometimes happen that some of the bins end up with zero
positive cases in them. And this obviously results in a calculation
error in the evaluation of the natural logarithm of the odds ratio.
GeneXproTools handles this with a slight modification to the Laplace
estimator to get what is called a complete Bayesian formulation with
prior probabilities. In essence, this means that when a particular
Quantile Table has bins with
only negative cases, then
we do the equivalent of priming all the bins with a very small
amount of positive cases.
The formula GeneXproTools uses in the evaluation of the Positives
Rate values pi for all the quantiles is the following:
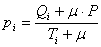
where μ is the Laplace estimator that in GeneXproTools has
the
value of 0.01; Qi and Ti are, respectively, the number of
Positive
Cases and the number of Total Cases in bin i; and P is the
Average Positive Rate of the whole dataset.
So, in the Log Odds Chart, the Log Odds values (adjusted or not with the Laplace strategy) are plotted on the Y-axis against the Model
Output in the X-axis. And as for Quantile Regression, here there are also special rules to follow, depending on whether the
predominant class is “1” or “0” and whether the model is normal or inverted. To be precise, the Log Odds are plotted against the
Model Upper Boundaries if the predominant class is “1” and the model is normal, or the
predominant class is “0” and the model is inverted; or against the
Lower Boundaries if the predominant class is “1” and the model is inverted, or the
predominant class is “0” and the model is normal.
Then a weighted linear regression is performed and the slope and
intercept of the regression line are evaluated. And these are the parameters that will be used in the
Logistic Regression Equation to evaluate the probabilities.
The regression line can be written as:
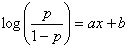
where p is the probability of being “1”; x is the Model Output; and
a and b are, respectively, the slope and intercept of the regression line. GeneXproTools draws the regression line and shows both the equation and the R-square in the
Log Odds Chart.
And now solving the logistic equation above for p, gives:
which is the formula for evaluating the probabilities with the
Logistic Regression Model. The probabilities estimated for each case are
shown in the Logistic Fit Table.
Besides the slope and intercept of the Logistic Regression Model, another useful and
widely used parameter is the exponent of the slope, usually represented by
Exp(slope). It describes the proportionate rate at which the predicted odds ratio changes with each successive unit of
x. GeneXproTools also shows this parameter both in the Log Odds Chart and in the
companion
Log Odds Stats Report.
 |
Logistic Fit Chart |
The Logistic Fit Chart is a very useful graph that allows not only a quick visualization of how good the
Logistic Fit is (the shape and steepness of the sigmoid curve are excellent indicators of the
robustness and accuracy of
the model), but also how the model outputs are distributed all over the
model range.
The blue line (the sigmoid curve) on the graph is the logistic transformation
of the model output x, using the
slope a and intercept b calculated in the Log Odds Chart and is evaluated by the already familiar formula for the probability p:
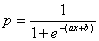
Since the proportion of Positive responses (1’s) and Negative
responses (0’s) must add up to 1, both probabilities can be read on
the vertical axis on the left. Thus, the probability of “1”
is read directly on the vertical axis; and the probability of “0”
is the distance from the line to the top of the graph, which is 1
minus the axis reading.
But there’s still more information on the Logistic Fit Chart. By plotting the dummy data
points, which consist of up to 1000 randomly selected model
scores paired with dummy random ordinates, one can clearly visualize
how model scores are distributed. Are they all clumped together or are
they finely distributed, which is the telltale sign of a good model?
This is valuable information not only to guide the modeling process
(not only in choosing model architecture and composition but also in
the exploration of different fitness
functions and class encodings that you can use to model your
data), but also to sharpen one’s intuition and knowledge about the
workings of learning evolutionary systems.
Indeed, browsing through the different models created in a run might
prove both insightful and great fun. And you can do that easily as
all the models in the Run History are accessible through the Model
selector box in the Logistic Regression Window. Good models will
generally allow for a good distribution of model outputs, resulting in a unique score
for each different case. Bad models, though, will usually
concentrate most of their responses around certain values and
consequently are unable to distinguish between most cases. These are
of course rough guidelines as the distribution of model outputs
depends on multiple factors, including the type and spread of input
variables and the complexity of the problem. For example, a simple
problem may be exactly solved by a simple step function.
Below is shown a Gallery of
Logistic Fit Charts typical of intermediate models generated during a GeneXproTools run.
It was generated using the same models used to create the
twin
ROC Curve Gallery
presented in the ROC Analysis section.
The models were created for a risk assessment problem with a training dataset with
18,253 cases and using a small population of just 30 programs.
The Classification Accuracy, the R-square, and the Area
Under the ROC Curve (AUC) of each model,
as well as the generation at which they were discovered, are also
shown as illustration.
From top to bottom, they are as follow:
- Generation 0, Accuracy = 65.33%, R-square = 0.0001, AUC = 0.5273
- Generation 5, Accuracy = 66.03%, R-square = 0.0173, AUC = 0.5834
- Generation 59, Accuracy = 66.92%, R-square = 0.0421, AUC = 0.6221
- Generation 75, Accuracy = 68.99%, R-square = 0.1076, AUC = 0.7068
- Generation 155, Accuracy = 69.93%, R-square = 0.1477, AUC = 0.7597
- Generation 489, Accuracy = 74.15%, R-square = 0.2445, AUC = 0.7968
|
 Generation 0, Accuracy = 65.33%, R-square = 0.0001, AUC = 0.5273
 Generation 5, Accuracy = 66.03%, R-square = 0.0173, AUC = 0.5834
 Generation 59, Accuracy = 66.92%, R-square = 0.0421, AUC = 0.6221
 Generation 75, Accuracy = 68.99%, R-square = 0.1076, AUC = 0.7068
 Generation 155, Accuracy = 69.93%, R-square = 0.1477, AUC = 0.7597
 Generation 489, Accuracy = 74.15%, R-square = 0.2445, AUC = 0.7968
Besides its main goal, which is to estimate the probability of a
response, the Logistic Regression Model can also be used to make
categorical or binary predictions.
From the logistic
regression equation introduced in the
previous section, we know that when a Positive event has the
same probability of happening as a Negative one, the log odds term
in the logistic regression equation becomes zero, giving:
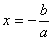
where x is the model output at the Logistic Cutoff
Point; and a and b are, respectively, the slope
and the intercept of the regression line.
The Logistic Cutoff Point can be obviously used to
evaluate a
Confusion Matrix (in the Logistic Regression Window it is called Logistic
Confusion Matrix to distinguish it from the
ROC Confusion Matrix), in which model scores with Prob[1] higher than or equal to 0.5
correspond to a
Positive case and a Negative otherwise.
In the Logistic Fit Table, GeneXproTools shows the Most
Likely Class, the Match, and Type values of the Logistic
Confusion Matrix (you can see the graphical representation of the
Logistic Confusion Matrix in the Confusion
Matrix Tab). For easy visualization, the model output closest to
the Logistic Cutoff Point is highlighted in light green in the
Logistic Fit Table. Note that the exact value of the Logistic Cutoff
Point is shown in the companion Logistic Fit Stats Report.
See Also:
Related Tutorials:
Related Videos:
|

