GeneXproTools 4.0 offers a total of 258 built-in
logical functions, including all the Boolean functions with one and two inputs, 92 functions with three inputs, and 146 functions with four
inputs, that can be used for designing logic circuits. This wide set of
logical functions allows the evolution of sophisticated logic
circuits that can be easily simplified and immediately ported to
different logical systems.
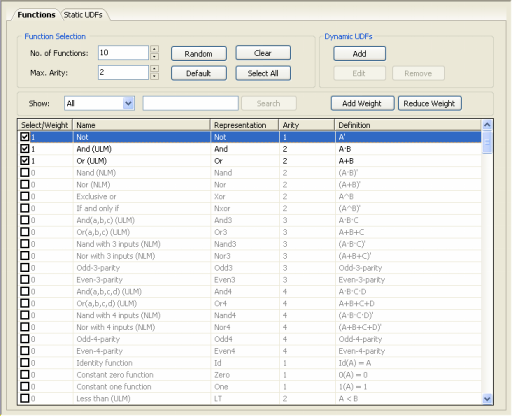
The Function
Selection Tool of GeneXproTools 4.0 helps you selecting different function sets very quickly
through the combination of the Show options with the
Random/Default/Clear/Select All buttons plus the Increase/Reduce
Weight buttons in the Functions
Panel. Furthermore, GeneXproTools automatically balances your
function set with the number of independent variables in your data,
which means that you just have to select the right functions for your problem and then choose their relative
proportions by adjusting their weights.
Despite the wide set of GeneXproTools built-in logical functions, some users sometimes want to model with different
ones.
GeneXproTools 4.0 gives the user the possibility of creating custom tailored functions
(Dynamic UDFs or DDFs) and evolve models with them. A note of
caution though: the use of DDFs slows considerably the evolutionary process and therefore should be used with moderation.
Below are listed all the 258 built-in logical functions available in GeneXproTools 4.0, including
their class (universal logical modules are identified by ULM,
whereas universal NAND-like modules are identified by NLM), their representation in
Karva Notation (shown
in red) and their logical definition (for more details about
their implementations, see the built-in
grammars of GeneXproTools):
Basic logical functions with 1 and 2 inputs:
- Not (Not): A'
- And (ULM) (And): A·B
- Or (ULM) (Or): A+B
- Nand (NLM) (Nand): (A·B)'
- Nor (NLM) (Nor): (A+B)'
- Exclusive or (Xor): A^B
- If and only if (Nxor): (A^B)'
Basic logical functions with 3 inputs:
- And(a,b,c) (ULM) (And3): A·B·C
- Or(a,b,c) (ULM) (Or3): A+B+C
- Nand with 3 inputs (NLM) (Nand3): (A·B·C)'
- Nor with 3 inputs (NLM) (Nor3): (A+B+C)'
- Odd-3-parity (Odd3): Odd-3-parity
- Even-3-parity (Even3): Even-3-parity
Basic logical functions with 4 inputs:
- And(a,b,c,d) (ULM) (And4): A·B·C·D
- Or(a,b,c,d) (ULM) (Or4): A+B+C+D
- Nand with 4 inputs (NLM) (Nand4): (A·B·C·D)'
- Nor with 4 inputs (NLM) (Nor4): (A+B+C+D)'
- Odd-4-parity (Odd4): Odd-4-parity
- Even-4-parity (Even4): Even-4-parity
Additional logical functions with 1 input:
- Identity function (Id): Id(A) = A
- Constant zero function (Zero): 0(A) = 0
- Constant one function (One): 1(A) = 1
Additional logical functions with 2 inputs:
- Less than (ULM) (LT): A < B
- Greater than (ULM) (GT): A > B
- Less or equal (ULM) (LOE): A <= B
- Greater or equal (ULM) (GOE): A >= B
- Not A (NotA): NOT(A,B) = NOT A
- Not B (NotB): NOT(A,B) = NOT B
- Input A (IdA): IdA(A,B) = A
- Input B (IdB): IdB(A,B) = B
- 0(a,b) (Zero2): 0(A,B) = 0
- 1(a,b) (One2): 1(A,B) = 1
Derived logical functions with 3 inputs:
- LT(a,b,c) (ULM) (LT3): A < B < C
- GT(a,b,c) (ULM) (GT3): A > B > C
- LOE(a,b,c) (ULM) (LOE3): A <= B <= C
- GOE(a,b,c) (ULM) (GOE3): A >= B >= C
Common logical functions with 3 inputs:
- 3-Multiplexer (ULM) (Mux): 3-Multiplexer
- If(a,b,c) (ULM) (If): If A = 1, then B, else C
- Majority(a,b,c) (ULM) (Maj): Majority(A,B,C)
- Minority(a,b,c) (ULM) (Min): Minority(A,B,C)
- Exactly two off (ULM) (2Off): Exactly two off
- Exactly two on (ULM) (2On): Exactly two on
Universal logical modules with 3 inputs (series A):
- ULM with 3 inputs (A1) (LM3A1): AC'+BC
- ULM with 3 inputs (A2) (LM3A2): AC'+B'C
- ULM with 3 inputs (A3) (LM3A3): A'C'+BC
- NLM with 3 inputs (A4) (LM3A4): A'C'+B'C
Universal logical modules with 3 inputs (series B):
- ULM with 3 inputs (B1) (LM3B1): (A+C')·(B+C)
- ULM with 3 inputs (B2) (LM3B2): (A+C')·(B'+C)
- ULM with 3 inputs (B3) (LM3B3): (A'+C')·(B+C)
- NLM with 3 inputs (B4) (LM3B4): (A'+C')·(B'+C)
Universal logical modules with 3 inputs (series C):
- ULM with 3 inputs (C1) (LM3C1): AB'+BC
- ULM with 3 inputs (C2) (LM3C2): AB'+ BC'
- ULM with 3 inputs (C3) (LM3C3): A'B'+BC
- NLM with 3 inputs (C4) (LM3C4): A'B'+ BC'
Universal logical modules with 3 inputs (series D):
- ULM with 3 inputs (D1) (LM3D1): (A+B')·(B+C)
- ULM with 3 inputs (D2) (LM3D2): (A+B')·(B+C')
- ULM with 3 inputs (D3) (LM3D3): (A'+B')·(B+C)
- NLM with 3 inputs (D4) (LM3D4): (A'+B')·(B+C')
Universal logical modules with 3 inputs (series E):
- ULM with 3 inputs (E1) (LM3E1): A'C+ AB'
- ULM with 3 inputs (E2) (LM3E2): A'C'+AB
- NLM with 3 inputs (E3) (LM3E3): A'C'+ AB'
Universal logical modules with 3 inputs (series F):
- ULM with 3 inputs (F1) (LM3F1): (A'+C)·(A+B')
- ULM with 3 inputs (F2) (LM3F2): (A'+C')·(A+B)
- NLM with 3 inputs (F3) (LM3F3): (A'+C')·(A+B')
Universal logical modules with 3 inputs (series G):
- ULM with 3 inputs (G1) (LM3G1): (A^C')·(B^C)
- ULM with 3 inputs (G2) (LM3G2): (A^C')·(B'^C)
- ULM with 3 inputs (G3) (LM3G3): (A'^C')·(B^C)
- ULM with 3 inputs (G4) (LM3G4): (A'^C')·(B'^C)
Universal logical modules with 3 inputs (series H):
- ULM with 3 inputs (H1) (LM3H1): ((A·B)'· C)'
- ULM with 3 inputs (H2) (LM3H2): (A·(B·C)')'
- ULM with 3 inputs (H3) (LM3H3): ((A+B)'+ C)'
- ULM with 3 inputs (H4) (LM3H4): (A+(B+C)')'
Comparison IF THEN ELSE functions with 3 inputs (series A):
- Less Than with 3 inputs (A) (NLM) (LT3A): If A < B, then (A·C),
else (B·C)'
- Greater Than with 3 inputs (A) (NLM) (GT3A): If A > B, then
(A·C), else (B·C)'
- Less Or Equal To with 3 inputs (A) (ULM) (LOE3A): If A <=
B, then (A·C), else (B·C)'
- Greater Or Equal To with 3 inputs (A) (ULM) (GOE3A): If A
>= B, then (A·C), else (B·C)'
- Equal To with 3 inputs (A) (ULM) (ET3A): If A = B, then (A·C),
else (B·C)'
- Not Equal To with 3 inputs (A) (NLM) (NET3A): If A != B, then
(A·C), else (B·C)'
Comparison IF THEN ELSE functions with 3 inputs (series B):
- Less Than with 3 inputs (B) (ULM) (LT3B): If A < B, then (A·C)',
else (A·C)
- Greater Than with 3 inputs (B) (ULM) (GT3B): If A > B, then
(A·C)', else (A·C)
- Less Or Equal To with 3 inputs (B) (NLM) (LOE3B): If A <=
B, then (A·C)', else (A·C)
- Greater Or Equal To with 3 inputs (B) (NLM) (GOE3B): If A
>= B, then (A·C)', else (A·C)
- Equal To with 3 inputs (B) (NLM) (ET3B): If A = B, then (A·C)',
else (A·C)
- Not Equal To with 3 inputs (B) (ULM) (NET3B): If A != B, then
(A·C)', else (A·C)
Comparison IF THEN ELSE functions with 3 inputs (series C):
- Less Than with 3 inputs (C) (ULM) (LT3C): If A < B, then (A+C)',
else (B+C)
- Greater Than with 3 inputs (C) (ULM) (GT3C): If A > B, then
(A+C)', else (B+C)
- Less Or Equal To with 3 inputs (C) (NLM) (LOE3C): If A <=
B, then (A+C)', else (B+C)
- Greater Or Equal To with 3 inputs (C) (NLM) (GOE3C): If A
>= B, then (A+C)', else (B+C)
- Equal To with 3 inputs (C) (NLM) (ET3C): If A = B, then (A+C)',
else (B+C)
- Not Equal To with 3 inputs (C) (ULM) (NET3C): If A != B, then
(A+C)', else (B+C)
Additional universal logical modules with 3 inputs:
- Rule 4 (ULM) (T004): 00000100
- Rule 8 (ULM) (T008): 00001000
- Rule 9 (NLM) (T009): 00001001
- Rule 32 (ULM) (T032): 00100000
- Rule 33 (NLM) (T033): 00100001
- Rule 41 (NLM) (T041): 00101001
- Rule 55 (NLM) (T055): 00110111
- Rule 57 (NLM) (T057): 00111001
- Rule 64 (ULM) (T064): 01000000
- Rule 65 (NLM) (T065): 01000001
- Rule 69 (NLM) (T069): 01000101
- Rule 73 (NLM) (T073): 01001001
- Rule 81 (NLM) (T081): 01010001
- Rule 89 (NLM) (T089): 01011001
- Rule 93 (NLM) (T093): 01011101
- Rule 96 (ULM) (T096): 01100000
- Rule 101 (NLM) (T101): 01100101
- Rule 109 (NLM) (T109): 01101101
- Rule 111 (NLM) (T111): 01101111
- Rule 121 (NLM) (T121): 01111001
- Rule 123 (NLM) (T123): 01111011
- Rule 125 (NLM) (T125): 01111101
- Rule 154 (ULM) (T154): 10011010
- Rule 223 (ULM) (T223): 11011111
- Rule 239 (ULM) (T239): 11101111
- Rule 249 (ULM) (T249): 11111001
- Rule 251 (ULM) (T251): 11111011
- Rule 253 (ULM) (T253): 11111101
Derived logical functions with 4 inputs:
- LT(a,b,c,d) (ULM) (LT4): A < B < C < D
- GT(a,b,c,d) (ULM) (GT4): A > B > C > D
- LOE(a,b,c,d) (ULM) (LOE4): A <= B <= C <= D
- GOE(a,b,c,d) (ULM) (GOE4): A >= B >= C >= D
Common logical functions with 4 inputs:
- Tie (ULM) (Tie): Tie
- Not tie (ULM) (Ntie): Not tie
- Exactly three off (ULM) (3Off): Exactly three off
- Exactly three on (ULM) (3On): Exactly three on
Universal logical modules with 4 inputs (series A):
- ULM with 4 inputs (A1) (LM4A1): AD'+BD+CD
- ULM with 4 inputs (A2) (LM4A2): AD'+B'D+CD
- ULM with 4 inputs (A3) (LM4A3): AD'+BD+C'D
- ULM with 4 inputs (A4) (LM4A4): AD'+B'D+C'D
- ULM with 4 inputs (A5) (LM4A5): A'D'+BD+CD
- ULM with 4 inputs (A6) (LM4A6): A'D'+B'D+CD
- ULM with 4 inputs (A7) (LM4A7): A'D'+BD+C'D
- NLM with 4 inputs (A8) (LM4A8): A'D'+B'D+C'D
Universal logical modules with 4 inputs (series B):
- ULM with 4 inputs (B1) (LM4B1): (A+D')·(B+D)·(C+D)
- ULM with 4 inputs (B2) (LM4B2): (A+D')·(B'+D)·(C+D)
- ULM with 4 inputs (B3) (LM4B3): (A+D')·(B+D)·(C'+D)
- ULM with 4 inputs (B4) (LM4B4): (A+D')·(B'+D)·(C'+D)
- ULM with 4 inputs (B5) (LM4B5): (A'+D')·(B+D)·(C+D)
- ULM with 4 inputs (B6) (LM4B6): (A'+D')·(B'+D)·(C+D)
- ULM with 4 inputs (B7) (LM4B7): (A'+D')·(B+D)·(C'+D)
- NLM with 4 inputs (B8) (LM4B8): (A'+D')·(B'+D)·(C'+D)
Universal logical modules with 4 inputs (series C):
- ULM with 4 inputs (C1) (LM4C1): AB'+BC+BD
- ULM with 4 inputs (C2) (LM4C2): AB'+B'C+BD
- ULM with 4 inputs (C3) (LM4C3): AB'+BC+B'D
- ULM with 4 inputs (C4) (LM4C4): AB'+B'C+B'D
- ULM with 4 inputs (C5) (LM4C5): A'B'+BC+BD
- ULM with 4 inputs (C6) (LM4C6): A'B'+B'C+BD
- ULM with 4 inputs (C7) (LM4C7): A'B'+BC+B'D
- NLM with 4 inputs (C8) (LM4C8): A'B'+B'C+B'D
Universal logical modules with 4 inputs (series D):
- ULM with 4 inputs (D1) (LM4D1): (A+B')·(B+C)·(B+D)
- ULM with 4 inputs (D2) (LM4D2): (A+B')·(B'+C)·(B+D)
- ULM with 4 inputs (D3) (LM4D3): (A+B')·(B+C)·(B'+D)
- ULM with 4 inputs (D4) (LM4D4): (A+B')·(B'+C)·(B'+D)
- ULM with 4 inputs (D5) (LM4D5): (A'+B')·(B+C)·(B+D)
- ULM with 4 inputs (D6) (LM4D6): (A'+B')·(B'+C)·(B+D)
- ULM with 4 inputs (D7) (LM4D7): (A'+B')·(B+C)·(B'+D)
- NLM with 4 inputs (D8) (LM4D8): (A'+B')·(B'+C)·(B'+D)
Universal logical modules with 4 inputs (series E):
- ULM with 4 inputs (E1) (LM4E1): AC'+BC+CD
- ULM with 4 inputs (E2) (LM4E2): AC'+B'C+CD
- ULM with 4 inputs (E3) (LM4E3): AC'+BC+C'D
- ULM with 4 inputs (E4) (LM4E4): AC'+B'C+C'D
- ULM with 4 inputs (E5) (LM4E5): A'C'+BC+CD
- ULM with 4 inputs (E6) (LM4E6): A'C'+B'C+CD
- ULM with 4 inputs (E7) (LM4E7): A'C'+BC+C'D
- NLM with 4 inputs (E8) (LM4E8): A'C'+B'C+C'D
Universal logical modules with 4 inputs (series F):
- ULM with 4 inputs (F1) (LM4F1): (A+C')·(B+C)·(C+D)
- ULM with 4 inputs (F2) (LM4F2): (A+C')·(B'+C)·(C+D)
- ULM with 4 inputs (F3) (LM4F3): (A+C')·(B+C)·(C'+D)
- ULM with 4 inputs (F4) (LM4F4): (A+C')·(B'+C)·(C'+D)
- ULM with 4 inputs (F5) (LM4F5): (A'+C')·(B+C)·(C+D)
- ULM with 4 inputs (F6) (LM4F6): (A'+C')·(B'+C)·(C+D)
- ULM with 4 inputs (F7) (LM4F7): (A'+C')·(B+C)·(C'+D)
- NLM with 4 inputs (F8) (LM4F8): (A'+C')·(B'+C)·(C'+D)
Universal logical modules with 4 inputs (series G):
- ULM with 4 inputs (G1) (LM4G1): A'D+AB+AC
- ULM with 4 inputs (G2) (LM4G2): A'D+AB'+AC
- ULM with 4 inputs (G3) (LM4G3): A'D+AB+ AC'
- ULM with 4 inputs (G4) (LM4G4): A'D+AB'+ AC'
- ULM with 4 inputs (G5) (LM4G5): A'D'+AB+AC
- ULM with 4 inputs (G6) (LM4G6): A'D'+AB'+AC
- ULM with 4 inputs (G7) (LM4G7): A'D'+AB+ AC'
- NLM with 4 inputs (G8) (LM4G8): A'D'+AB'+ AC'
Universal logical modules with 4 inputs (series H):
- ULM with 4 inputs (H1) (LM4H1): (A'+D)·(A+B)·(A+C)
- ULM with 4 inputs (H2) (LM4H2): (A'+D)·(A+B')·(A+C)
- ULM with 4 inputs (H3) (LM4H3): (A'+D)·(A+B)·(A+C')
- ULM with 4 inputs (H4) (LM4H4): (A'+D)·(A+B')·(A+C')
- ULM with 4 inputs (H5) (LM4H5): (A'+D')·(A+B)·(A+C)
- ULM with 4 inputs (H6) (LM4H6): (A'+D')·(A+B')·(A+C)
- ULM with 4 inputs (H7) (LM4H7): (A'+D')·(A+B)·(A+C')
- NLM with 4 inputs (H8) (LM4H8): (A'+D')·(A+B')·(A+C')
Universal logical modules with 4 inputs (series I):
- NLM with 4 inputs (I1) (LM4I1): (((A·B)'·C)'· D)'
- NLM with 4 inputs (I2) (LM4I2): (A·(B·(C·D)')')'
- NLM with 4 inputs (I3) (LM4I3): ((A·(B· C)')'·D)'
- NLM with 4 inputs (I4) (LM4I4): (A·((B·C)'· D)')'
- NLM with 4 inputs (I5) (LM4I5): (((A+B)'+C)'+ D)'
- NLM with 4 inputs (I6) (LM4I6): (A+(B+(C+D)')')'
- NLM with 4 inputs (I7) (LM4I7): ((A+(B+ C)')'+D)'
- NLM with 4 inputs (I8) (LM4I8): (A+((B+C)'+ D)')'
Comparison IF THEN ELSE functions with 4 inputs (series A):
- Less Than with 4 inputs (A) (ULM) (LT4A): If A < B, then C,
else D
- Greater Than with 4 inputs (A) (ULM) (GT4A): If A > B, then
C, else D
- Less Or Equal To with 4 inputs (A) (ULM) (LOE4A): If A <=
B, then C, else D
- Greater Or Equal To with 4 inputs (A) (ULM) (GOE4A): If A
>= B, then C, else D
- Equal To with 4 inputs (A) (ULM) (ET4A): If A = B, then C,
else D
- Not Equal To with 4 inputs (A) (ULM) (NET4A): If A != B, then
C, else D
Comparison IF THEN ELSE functions with 4 inputs (series B):
- Less Than with 4 inputs (B) (NLM) (LT4B): If A < B, then (C·D),
else D'
- Greater Than with 4 inputs (B) (NLM) (GT4B): If A > B, then
(C·D), else D'
- Less Or Equal To with 4 inputs (B) (ULM) (LOE4B): If A <=
B, then (C·D), else D'
- Greater Or Equal To with 4 inputs (B) (ULM) (GOE4B): If A
>= B, then (C·D), else D'
- Equal To with 4 inputs (B) (ULM) (ET4B): If A = B, then (C·D),
else D'
- Not Equal To with 4 inputs (B) (NLM) (NET4B): If A != B, then
(C·D), else D'
Comparison IF THEN ELSE functions with 4 inputs (series C):
- Less Than with 4 inputs (C) (NLM) (LT4C): If A < B, then (C+D),
else D'
- Greater Than with 4 inputs (C) (NLM) (GT4C): If A > B, then
(C+D), else D'
- Less Or Equal To with 4 inputs (C) (ULM) (LOE4C): If A <=
B, then (C+D), else D'
- Greater Or Equal To with 4 inputs (C) (ULM) (GOE4C): If A
>= B, then (C+D), else D'
- Equal To with 4 inputs (C) (ULM) (ET4C): If A = B, then (C+D),
else D'
- Not Equal To with 4 inputs (C) (NLM) (NET4C): If A != B, then
(C+D), else D'
Comparison IF THEN ELSE functions with 4 inputs (series D):
- Less Than with 4 inputs (D) (NLM) (LT4D): If A < B, then (A·D),
else (C·D)'
- Greater Than with 4 inputs (D) (NLM) (GT4D): If A > B, then
(A·D), else (C·D)'
- Less Or Equal To with 4 inputs (D) (ULM) (LOE4D): If A <=
B, then (A·D), else (C·D)'
- Greater Or Equal To with 4 inputs (D) (ULM) (GOE4D): If A
>= B, then (A·D), else (C·D)'
- Equal To with 4 inputs (D) (ULM) (ET4D): If A = B, then (A·D),
else (C·D)'
- Not Equal To with 4 inputs (D) (NLM) (NET4D): If A != B, then
(A·D), else (C·D)'
Comparison IF THEN ELSE functions with 4 inputs (series E):
- Less Than with 4 inputs (E) (ULM) (LT4E): If A < B, then (A·D)',
else (A·C)
- Greater Than with 4 inputs (E) (ULM) (GT4E): If A > B, then
(A·D)', else (A·C)
- Less Or Equal To with 4 inputs (E) (NLM) (LOE4E): If A <=
B, then (A·D)', else (A·C)
- Greater Or Equal To with 4 inputs (E) (NLM) (GOE4E): If A
>= B, then (A·D)', else (A·C)
- Equal To with 4 inputs (E) (NLM) (ET4E): If A = B, then (A·D)',
else (A·C)
- Not Equal To with 4 inputs (E) (ULM) (NET4E): If A != B, then
(A·D)', else (A·C)
Additional universal logical modules with 4 inputs:
- Rule 00002 (ULM) (Q0002): 0000000000000010
- Rule 00028 (ULM) (Q001C): 0000000000011100
- Rule 00072 (ULM) (Q0048): 0000000001001000
- Rule 02048 (ULM) (Q0800): 0000100000000000
- Rule 13176 (ULM) (Q3378): 0011001101111000
- Rule 13429 (NLM) (Q3475): 0011010001110101
- Rule 15536 (ULM) (Q3CB0): 0011110010110000
- Rule 15855 (NLM) (Q3DEF): 0011110111101111
- Rule 15871 (NLM) (Q3DFF): 0011110111111111
- Rule 16896 (ULM) (Q4200): 0100001000000000
- Rule 19473 (NLM) (Q4C11): 0100110000010001
- Rule 20736 (ULM) (Q5100): 0101000100000000
- Rule 24303 (NLM) (Q5EEF): 0101111011101111
- Rule 24319 (NLM) (Q5EFF): 0101111011111111
- Rule 27245 (NLM) (Q6A6D): 0110101001101101
- Rule 28533 (NLM) (Q6F75): 0110111101110101
- Rule 29892 (ULM) (Q74C4): 0111010011000100
- Rule 32163 (NLM) (Q7DA3): 0111110110100011
- Rule 33540 (ULM) (Q8304): 1000001100000100
- Rule 33840 (ULM) (Q8430): 1000010000110000
- Rule 34115 (ULM) (Q8543): 1000010101000011
- Rule 40320 (ULM) (Q9D80): 1001110110000000
- Rule 41106 (ULM) (QA092): 1010000010010010
- Rule 45930 (ULM) (QB36A): 1011001101101010
- Rule 52175 (ULM) (QCBCF): 1100101111001111
- Rule 61105 (ULM) (QEEB1): 1110111010110001
- Rule 61439 (ULM) (QEFFF): 1110111111111111
- Rule 65403 (ULM) (QFF7B): 1111111101111011
- Rule 65526 (ULM) (QFFF6): 1111111111110110
- Rule 65531 (ULM) (QFFFB): 1111111111111011
By selecting the Functions Tab in the Functions
Panel, you have full access to the 258 built-in logical functions of
GeneXproTools 4.0. Here is also the place where you can add Dynamic UDFs to your modeling kit.
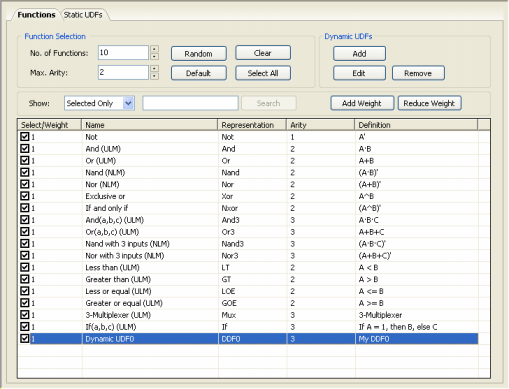
To select a function, just check the box on the left. By default, the weight of each function is 1, but you can increase the probability of a function being included in your
logic circuits by increasing its weight in the Select/Weight column. GeneXproTools automatically balances your
function set with the number of independent variables in your data,
so now you just have to select the right functions for your problem and then choose their relative
proportions by choosing their weights.
To add a DDF to your modeling kit, just click the Add button on the Dynamic UDFs frame and the
DDF Editor appears.
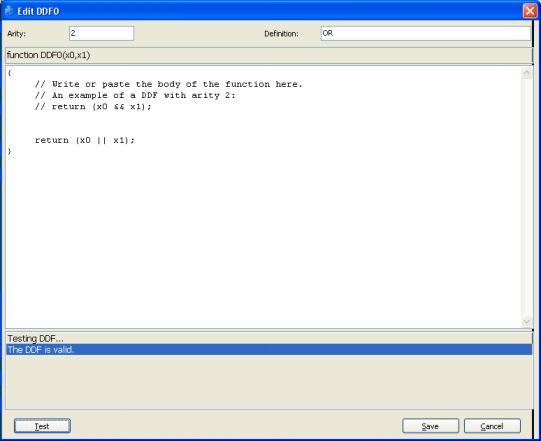
By choosing the arity (minimum is 1 and maximum is 4) in the Arity box, the function header appears below. Then you just have to write the body of the function in the code editor. The code must be in JavaScript and can be
conveniently tested for compiling errors by pressing the Test button.
In the Definition box, you can write a brief description of the function for your future reference. The text you write
there will appear in the Definition column.
Dynamic UDFs are extremely powerful and interesting tools as they are treated exactly like the built-in functions of
GeneXproTools and therefore can be used to model all kinds of relationships between variables or complex expressions. For instance, you can design a DDF so that it will model four
expressions OR-ed together, that is, DDF = (expression 1) OR (expression 2)
OR (expression 3) OR (expression 4), where the value of each expression will depend on the context of the DDF in the expression tree. A note of caution, though, although extremely interesting, DDFs decrease considerably the speed of the algorithm and therefore we advise you to choose your functions from the wide set of
GeneXproTools 4.0 built-in logical functions.
|


