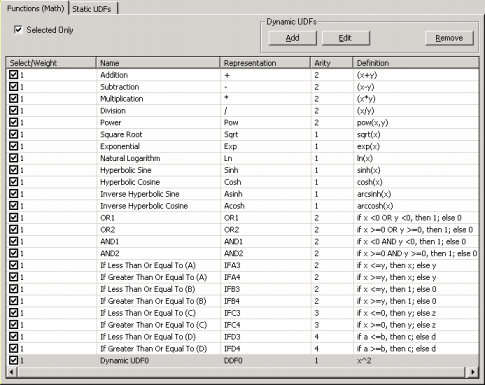
| By selecting the Functions (Math)
Tab, you have full access to the 70 built-in mathematical functions of APS 3.0, including 24 IF THEN ELSE rules. Here is also the place where you can add
Dynamic UDFs (DDFs) to your modeling kit.
To select a function, just check the box on the left. By default, the weight of each function is 1, but you can increase the probability of a function being included in your models by increasing its weight in the Select/Weight column. The weight property is very important for a successful modeling, as the overall number of functions used in a run must be well balanced with the number of terminals or variables in your data. For instance, if you are modeling data with hundreds of variables and using only the four arithmetical operators, you must weight proportionately the representation of each function in the function set, otherwise the creation of complex models will be seriously compromised. A good rule of thumb, is to have at least as many functions in the function set as there are variables.
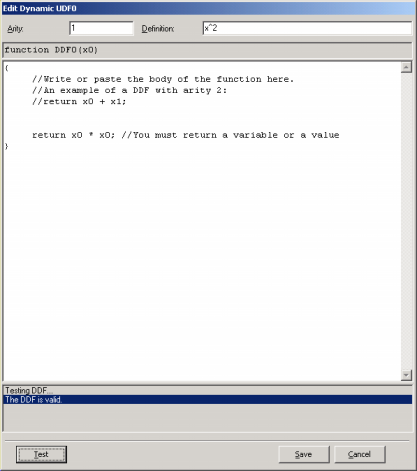
By choosing the arity (minimum is 1 and maximum is 4) in the Arity box, the function header appears below. Then you just have to write the body of the function in the code editor. The code must be in JavaScript and can be rapidly tested for compiling errors. |