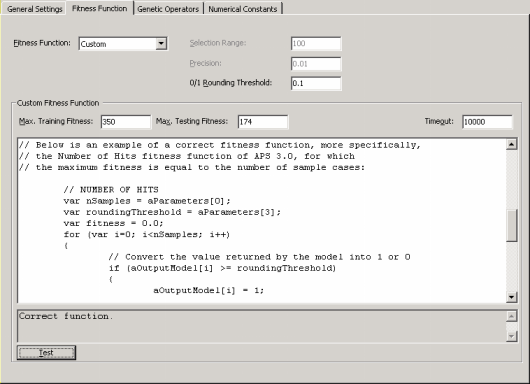
For all classification problems, in order to be able to apply a particular fitness function, the
learning algorithms APS 3.0 must convert the value returned by the evolved model into “1” or “0” using the
0/1 Rounding Threshold. If the value returned by the evolved model is equal to or greater than the rounding threshold, then the record is classified as “1”, “0” otherwise.
Thus, the 0/1 Rounding Threshold is an integral part of all fitness functions used for classification and must be appropriately set in the Settings Panel -> Fitness Function Tab.
The PPV/NPV fitness function of APS 3.0 is, as expected, based both on the
positive predictive value (PPV) and
negative predictive value (NPV).
The PPV/NPV PNi of an individual program i is evaluated by the equation:
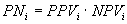
where PPVi is the positive predictive value and
NPVi is the negative predictive value of the individual program
i, and are given by the formulas:
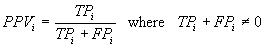

where TPi, TNi, FPi, and
FNi represent, respectively, the number of true
positives, true negatives, false positives, and false
negatives.
TPi, TNi, FPi, and
FNi are the four different possible outcomes of a single prediction for a two-class case with classes “1” (“yes”) and “0” (“no”). A
false positive is when the outcome is incorrectly classified as “yes” (or “positive”), when it is in fact “no” (or “negative”). A
false negative is when the outcome is incorrectly classified as negative when it is in fact positive.
True positives and true negatives are obviously correct classifications.
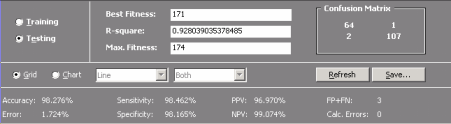
Keeping track of all these possible outcomes is such an error-prone activity, that they are usually shown in what is called a
confusion matrix. And for all classification problems, regardless of the fitness function, APS 3.0 shows the confusion matrix for all the evolved models.

Thus, for evaluating the fitness fi of an individual program
i, the following equation is used:
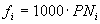
which obviously ranges from 0 to 1000, with 1000 corresponding to the ideal (the coefficient 1000 allows a fairer distribution of fitnesses for selection).
|