Random numerical constants (RNCs) can be easily implemented in gene expression
programming (GEP). For that an additional domain Dc is introduced in GEP
genes. Structurally, the Dc comes after the
tail, has a length t equal to
the length of the tail, and is composed of the symbols used to represent the random constants. Therefore, another region (besides the
head and tail) with defined boundaries and its own alphabet is created in the gene.
Although this extra domain Dc is essential for handling numerical
constants, APS 3.0 hides the Dc from the user and takes care of all
the decoding. However, if you want to understand the workings of
essential features for fine-tuning numerical constants such as
special genetic operators and initial diversity of random numerical
constants, it's a plus if you know a little about its structure and
organization.
For each gene the numerical constants are randomly generated at the beginning of a run, but their circulation is guaranteed by the usual genetic operators of
mutation, transposition,
inversion, and recombination. Besides, a special mutation operator
(RNC mutation) allows the permanent introduction of variation in the set of random constants; and three Dc specific operators –
Dc Mutation, Dc IS
transposition, and Dc inversion – guarantee the effective shuffling of the constants through the programs of the population.
Consider the single-gene chromosome with a head size h = 7 (the Dc is shown in
blue):
01234567890123456789012
+?*+?**aaa??aaa68083295
where the terminal “?” represents the random constants. The expression of this kind of chromosome is done exactly as
in the basic gene expression algorithm, obtaining:
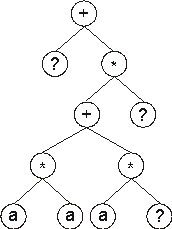
Then the ?’s in the expression tree (ET) are replaced from left to right and from top to bottom by the symbols (numerals, for simplicity) in Dc, obtaining:
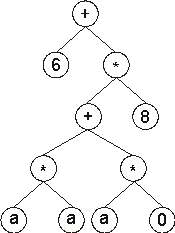
The values corresponding to these symbols are kept in an array. For simplicity, the number represented by the numeral indicates the order in the array. For instance, for the 10 elements array:
A = {0.611, 1.184, 2.449, 2.98, 0.496, 2.286, 0.93, 2.305, 2.737, 0.755}
the chromosome above gives:
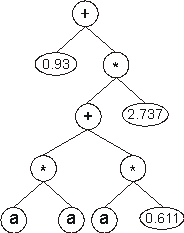
Obviously, the GEP-RNC algorithm can also be used to evolve highly sophisticated programs composed of multiple sub-programs through the use of
multigenic chromosomes. The only difference is that the genes in the GEP-RNC algorithm carry an extra domain for encoding the random numerical constants.
|


