| The chromosome architecture of your models include the
head size, the number of genes and the linking
function. You choose these parameters in the Settings Panel -> General Settings.
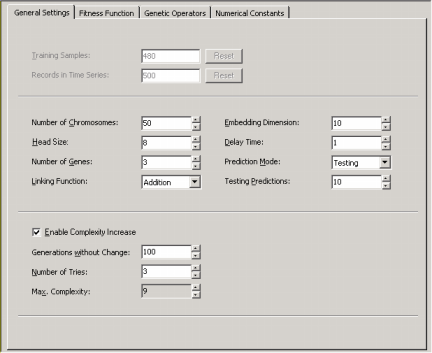
The Head Size determines the complexity of each term in your model. In the
heads of genes, the APS learning algorithm tries out different arrangements of functions and
terminals (variables and constants) in order to model your data. The plasticity of this architecture allows the discovery of
a virtually infinite number of models of different sizes and shapes which are afterwards tested and selected during the learning process.
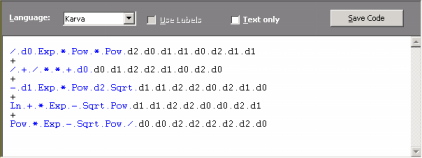
More specifically, the head size h of each gene determines the maximum width
w and maximum depth d of the sub-expression trees
encoded in the gene, which are given by the formulas:
w = (n - 1) * h + 1
d = (h + 1) / m * (m + 1)/2
where m is minimum arity and n is maximum arity.
Thus, the APS learning algorithm selects its models between these extreme cases, fine-tuning the ideal size and shape during the evolutionary process without human intervention.
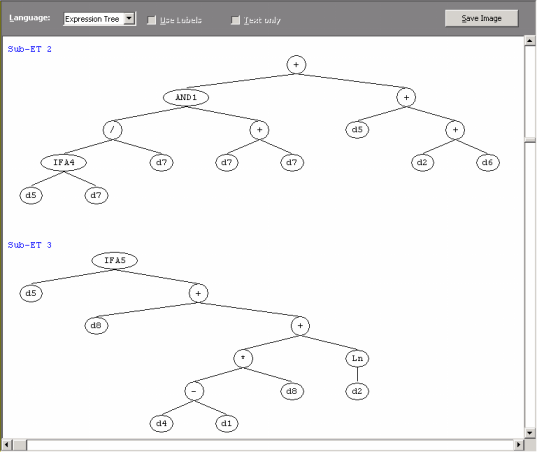
The number of genes per chromosome is also an important parameter. It will determine the number of (complex) terms in your model as each gene codes for a different
parse tree (sub-expression tree or sub-ET). Theoretically, one could just use a huge single gene in order to evolve very complex models. But the partition of the chromosome into simpler, more manageable units gives an edge to the learning process and more efficient and elegant models can be discovered using
multigenic chromosomes.
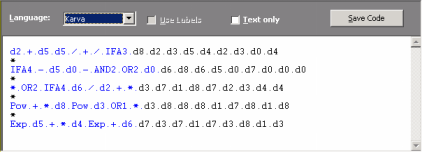
Whenever the number of genes is greater than one, you must also choose a suitable
linking function for linking the mathematical terms encoded in each gene. APS 3.0 allows you to choose
addition, subtraction, multiplication, or division to link the
sub-ETs. As expected, addition (and obviously subtraction) works very well for virtually all problems but sometimes one of the other linkers could be useful for searching different solution spaces and finding a very good, albeit unexpected model.
|